What is Trigonometry?
Trigonometry is the branch of mathematics that studies relationships between the angles and sides of triangles—especially right-angled triangles.
It focuses on three main ratios: sine (sin), cosine (cos), and tangent (tan).
Parts of a Right-Angled Triangle
Consider a right-angled triangle with angle θ (theta):
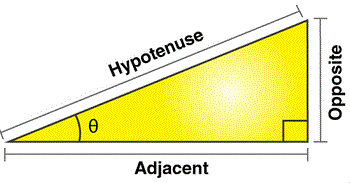
Hypotenuse: the longest side, opposite the right angle
Opposite side: the side opposite angle θ
Adjacent side: the side next to angle θ (but not the hypotenuse)
To remember the ratios, use:
SOH-CAH-TOA
Sine = Opposite / Hypotenuse
Cosine = Adjacent / Hypotenuse
Tangent = Opposite / Adjacent
The Three Primary Ratios
(a) Sine (sin θ)
sinθ = Opposite/Hypotenuse
(b) Cosine (cos θ)
cosθ = Adjacent/Hypotenuse
(c) Tangent (tan θ)
tanθ = Opposite/Adjacent
How the Ratios Work (Example)
Suppose you have a right-angled triangle where:
Opposite side = 5 cm
Adjacent side = 12 cm
Hypotenuse = 13 cm
Then:
Sine sinθ = 5/13
Cosine cosθ = 12/13
Tangent tanθ = 5/12
Using Trig Ratios to Find Missing Sides
Example:
Angle θ = 30°, hypotenuse = 10 cm. Find the opposite side.
sin30° = Opposite/10
0.5 = Opposite/10
Opposite = 5 cm
Using Trig Ratios to Find Missing Angles
Example:
Opposite = 8 cm, Hypotenuse = 17 cm. Find θ.
![]()
Use the inverse sine (sin⁻¹):
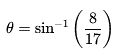
Calculator gives approximately: θ≈28°
Practice Questions
1. In a right triangle, opposite = 7 cm, adjacent = 24 cm. Find tan θ.
2. In a right triangle, Angle θ = 60°, hypotenuse = 12 cm. Find the opposite side.
3. In a right triangle, Opposite = 10 cm, hypotenuse = 26 cm. Find θ.
4. In a right triangle, Adjacent = 15 cm, angle = 35°. Find the hypotenuse.